«Математик так же, как художник или поэт, создает узоры. И если его узоры более устойчивы, то лишь потому, что они составлены из идей... Узоры математика так же, как узоры художника или поэта, должны быть прекрасны; идеи так же, как цвета или слова, должны соответствовать друг другу. Красота есть первое требование: в мире нет места для некрасивой математики ».
Г.Х.Харди
В первой главе отмечалось, что существуют первообразные довольно простых функций, которые уже нельзя выразить через элементарные функции. В связи с этим, огромное практическое значение приобретают те классы функций, о которых можно точно сказать, что их первообразные – элементарные функции. К такому классу функций относятся рациональные функции , представляющие собой отношение двух алгебраических многочленов. К интегрированию рациональных дробей приводят многие задачи. Поэтому очень важно уметь интегрировать такие функции.
2.1.1. Дробно-рациональные функции
Рациональной дробью (или дробно-рациональной функцией )называется отношение двух алгебраических многочленов:
где и – многочлены.
Напомним, что многочленом (полиномом , целой рациональной функцией ) n -й степени называется функция вида
где
– действительные числа. Например,
– многочлен первой степени;
– многочлен четвертой степени и т.д.
Рациональная дробь (2.1.1) называется правильной , если степень ниже степени , т.е. n <m , в противном случае дробь называется неправильной .
Любую неправильную дробь можно представить в виде суммы многочлена (целой части) и правильной дроби (дробной части). Выделение целой и дробной частей неправильной дроби можно производить по правилу деления многочленов «уголком».
Пример 2.1.1. Выделить целую и дробную части следующих неправильных рациональных дробей:
а) 
, б) 
.
Решение . а) Используя алгоритм деления «уголком», получаем
Таким образом, получаем
.
б) Здесь также используем алгоритм деления «уголком»:
В результате, получаем
.
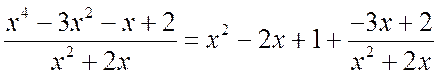Подведём итоги. Неопределённый интеграл от рациональной дроби в общем случае можно представить суммой интегралов от многочлена и от правильной рациональной дроби. Нахождение первообразных от многочленов не представляет трудностей. Поэтому в дальнейшем будем рассматривать в основном правильные рациональные дроби.
2.1.2. Простейшие рациональные дроби и их интегрирование
Среди правильных рациональных дробей выделяют четыре типа, которые относят кпростейшим (элементарным) рациональным дробям:
|
3) |
4) |
,
,где – целое число, 
, т.е. квадратный трёхчлен 
не
имеет действительных корней.
Интегрирование простейших дробей 1-го и 2-го типа не представляет больших трудностей:
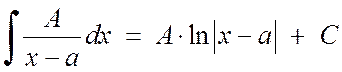, (2.1.3)
. (2.1.4)
Рассмотрим теперь интегрирование простейших дробей 3-го типа, а дроби 4-го типа рассматривать не будем.
Начнём с интегралов вида
.
Данный интеграл обычно вычисляют путем выделения полного квадрата в знаменателе. В результате получается табличный интеграл следующего вида
или 
.
Пример 2.1.2. Найти интегралы:
а)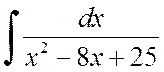 
, б) 
.
Решение . а) Выделим из квадратного трёхчлена полный квадрат:
Отсюда находим
б) Выделив из квадратного трёхчлена полный квадрат, получаем:
Таким образом,
.
Для нахождения интеграла
можно
выделить в числителе производную знаменателя и разложить интеграл на сумму двух
интегралов: первый из них подстановкой 
сводится
к виду
,
а второй – к рассмотренному выше.
Пример 2.1.3. Найти интегралы:
.
Решение
. Заметим,
что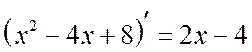 
. Выделим в числителе производную
знаменателя:
Первый
интеграл вычисляется при помощи подстановки 
:
Во втором интеграле выделим полный квадрат в знаменателе
Окончательно, получаем
2.1.3. Разложение правильной рациональный
дроби
на сумму простейших дробей
Любую правильную рациональную дробь 
можно представить единственным
образом в виде суммы простейших дробей. Для этого знаменатель нужно разложить на множители. Из высшей алгебры известно, что каждый многочлен с
действительными коэффициентами
Ранее речь шла об общих приемах интегрирования. В этом и следующих параграфах мы будем говорить об интегрировании конкретных классов функций с помощью рассмотренных приемов.
Интегрирование простейших рациональных функций
Рассмотрим интеграл вида \textstyle{\int R(x)\,dx} , где y=R(x) - рациональная функция. Всякое рациональное выражение R(x) можно представить в виде \frac{P(x)}{Q(x)} , где P(x) и Q(x) - многочлены. Если эта дробь неправильная, т. е. если степень числителя больше или равна степени знаменателя, то ее можно представить в виде суммы многочлена (целая часть) и правильной дроби. Поэтому достаточно рассмотреть интегрирование правильных дробей.
Покажем, что интегрирование таких дробей сводится к интегрированию простейших дробей , т. е. выражений вида:
\mathsf{1)}~\frac{A}{x-a};\quad \mathsf{2)}~\frac{A}{(x-a)^n};\quad \mathsf{3)}~ \frac{Ax+B}{x^2+px+q};\quad \mathsf{4)}~\frac{Ax+B}{(x^2+px+q)^n}.
где A,\,B,\,a,\,p,\,q - действительные числа, а квадратный трехчлен x^2+px+q не имеет действительных корней. Выражения вида 1) и 2) называют дробями 1-го рода, а выражения вида 3) и 4) - дробями 2-го рода.
Интегралы от дробей 1-го рода вычисляются непосредственно
\begin{aligned}\mathsf{1)}&~\int\frac{A}{x-a}\,dx= A\ln|x-a|+C;\\ \mathsf{2)}&~ \int\frac{A}{(x-a)^n}\,dx= A\int(x-a)^{-n}\,dx= A\,\frac{(x-a)^{-n+1}}{-n+1}+C~(n=2,3,4,\ldots). \end{aligned}
Рассмотрим вычисление интегралов от дробей 2-го рода: \mathsf{3)}~ \int\frac{Ax+B}{x^2+px+q}\,dx\,.
Сначала заметим, что
\int\frac{dt}{t^2+a^2}= \frac{1}{a}\operatorname{arctg}\frac{t}{a}+C,\qquad \int\frac{t\,dt}{t^2+a^2}= \frac{1}{2}\ln(t^2+a^2)+C.
Чтобы свести вычисление интеграла 3) к этим двум интегралам, преобразуем квадратный трехчлен x^2+px+q , выделив из него полный квадрат:
x^2+px+q= {\left(x+\frac{p}{2}\right)\!}^2+ \left(q-\frac{p^2}{4}\right)\!.
Так как по предположению этот трехчлен не имеет действительных корней, то q-\frac{p^2}{4}>0 и мы можем положить q-\frac{p^2}{4}=a^2 . Подстановка x+\frac{p}{2}=t,~ dx=dt преобразует интеграл 3) к линейной комбинации указанных двух интегралов:
\begin{aligned}\int\frac{Ax+B}{x^2+px+q}\,dx&= \int\frac{A\!\left(t-\frac{p}{2}\right)+B}{t^2+a^2}\,dt= A\int\frac{t\,dt}{t^2+a^2}+ \left(B-\frac{Ap}{2}\right)\!\int\frac{dt}{t^2+a^2}=\\ &=\frac{A}{2}\ln(t^2+a^2)+ \frac{1}{a}\!\left(B-\frac{Ap}{2}\right)\!\ \operatorname{arctg}\frac{t}{a}+C. \end{aligned}
В окончательном ответе нужно лишь заменить {t} на x+\frac{p}{2} , а {a} на \sqrt{q-\frac{p^2}{4}} . Так как t^2+a^2=x^2+px+q , то
\int\frac{Ax+B}{x^2+px+q}\,dx= \frac{A}{2}\ln(x^2+px+q)+ \frac{B-\dfrac{Ap}{2}}{\sqrt{q-\dfrac{p^2}{4}}} \operatorname{arctg}\frac{x+\dfrac{p}{2}}{\sqrt{q-\dfrac{p^2}{4}}}+C.
Рассмотрим случай \mathsf{4)}~ \int\frac{Ax+B}{(x^2+px+q)^n}\,dx .
Как и в предыдущем случае, положим x+\frac{p}{2}=t . Получим:
\int\frac{Ax+B}{(x^2+px+q)^n}\,dx= A\int\frac{t\,dt}{(t^2+a^2)^n}+ \left(B-\frac{Ap}{2}\right)\! \int\frac{dt}{(t^2+a^2)^n}\,.
Первое слагаемое вычисляется так:
A\int\frac{t\,dt}{(t^2+a^2)^n}= \frac{A}{2}\int(t^2+a^2)^{-n}\,d(t^2+a^2)= \frac{A}{2}\frac{(t^2+a^2)^{-n+1}}{-n+1}= \frac{A}{2(1-n)(t^2+a^2)^{n-1}}\,.
Второй же интеграл вычисляется с помощью рекуррентной формулы.
Пример 1. Вычислим \int\frac{3x+2}{x^2+2x+3}\,dx .
Решение. Имеем: x^2+2x+3=(x+1)^2+2 . Положим x+1=t . Тогда dx=dt и 3x+2=3(t-1)+2=3t-1 и, следовательно,
\begin{aligned}\int\frac{3x+2}{x^2+2x+3}\,dx&= \int\frac{3t-1}{t^2+2}\,dt= \frac{3}{2}\int\frac{2t\,dt}{t^2+2}- \int\frac{dt}{t^2+(\sqrt{2})^2}=\\ &=\frac{3}{2}\ln(t^2+2)- \frac{1}{\sqrt{2}}\operatorname{arctg}\frac{t}{\sqrt{2}}+C=\\ &=\frac{3}{2}\ln(x^2+2x+3)- \frac{1}{\sqrt{2}}\operatorname{arctg}\frac{x+1}{\sqrt{2}}+C. \end{aligned}
Пример 2. Вычислим \int\frac{x+2}{(x^2+6x+10)^2}\,dx .
Решение. Имеем: x^2+6x+10=(x+3)^2+1 . Введем новую переменную, положив x+3=t . Тогда dt=dx и x+2=t-1 . Заменив переменную под знаком интеграла, получим:
\begin{aligned}\int\frac{x+2}{(x^2+6x+10)^2}\,dx&= \int\frac{t-1}{(t^2+1)^2}\,dt= \frac{1}{2}\int\frac{2t\,dt}{(t^2+1)^2}-\int\frac{dt}{(t^2+1)^2}=\\ &=-\frac{1}{2(t^2+1)}- \int\frac{dt}{(t^2+1)^2}\,. \end{aligned}}
Положим I_2=\int\frac{dt}{(t^2+1)^2} . Имеем:
I_2=\frac{1}{2}I_1+\frac{1}{2}\frac{t}{t^2+1} , но I_1=\int\frac{dt}{t^2+1}= \operatorname{arctg}t Таким образом, I_2= \frac{1}{2}\operatorname{arctg}t+ \frac{t}{2(t^2+1)} .
Окончательно получаем:
\begin{aligned}\int\frac{x+2}{(x^2+6x+10)^2}\,dx&=-\frac{1}{2(t^2+1)}-\frac{1}{2}\operatorname{arctg}t-\frac{t}{2(t^2+1)}=\\ &=-\frac{1}{2(x^2+6x+10)}- \frac{1}{2}\operatorname{arctg}(x+3)- \frac{x+3}{2(x^2+6x+10)}+C=\\ &=\frac{-x-4}{2(x^2+6x+10)}-\frac{1}{2}\operatorname{arctg}(x+3)+C \end{aligned}
Интегрирование правильных дробей
Рассмотрим правильную дробь R(x)=\frac{P(x)}{Q(x)} , где Q(x) - многочлен степени n . Не теряя общности, можно считать, что старший коэффициент в Q(x) равен 1. В курсе алгебры доказывается, что такой многочлен с действительными коэффициентами может быть разложен на множители первой и второй степени с действительными коэффициентами:
Q(x)= (x-x_1)^{\alpha}\ldots (x-x_k)^{\beta} (x^2+p\,x+q)^{\gamma}\ldots (x^2+r\,x+s)^{\delta}.
где x_1,\ldots,x_k -действительные корни многочлена Q(x) , а квадратные трехчлены не имеют действительных корней. Можно доказать, что тогда R(x) представляется в виде суммы простейших дробей вида 1) -4):
\begin{aligned}R(x)=&\frac{P(x)}{Q(x)}= \frac{A_1}{(x-x_1)^{\alpha}}+ \frac{A_2}{(x-x_1)^{\alpha-1}}+\ldots+ \frac{A_{\alpha}}{x-x_1}\,+\\ &+\,\ldots+ \frac{B_1}{(x- x_k)^{\beta}}+ \frac{B_2}{(x-x_k)^{\beta-1}}+\ldots+ \frac{B_{\beta}}{x-x_k}+ \frac{M_1x+ N_1}{(x^2+p\,x+q)^{\gamma}}\,+\\ &+\,\ldots+ \frac{M_{\gamma}+ N_{\gamma}}{x^2+ p\,x+s}+ \frac{E_1x+F_1}{(x^2+rx+s)^{\delta}}+\ldots+ \frac{E_{\delta}x+F_{\delta}}{x^2+rx+s}\, \end{aligned}
где показатели у знаменателей последовательно уменьшаются от \alpha до 1, …, от \beta до 1, от \gamma до 1, …, от \delta до 1, а A_1,\ldots,F_{\delta} - неопределенные коэффициенты. Для того чтобы найти эти коэффициенты, необходимо освободиться от знаменателей и, получив равенство двух многочленов, воспользоваться методом неопределенных коэффициентов.
Другой способ определения коэффициентов A_1,\ldots, A_{\alpha}, \ldots, F_{\delta} основан на подстановке значений переменной x . Подставляя в равенство, полученное из равенства (1) после освобождения от знаменателей, вместо x любое число, придем к линейному уравнению относительно искомых коэффициентов. Путем подстановки необходимого количества таких частных значений переменной получим систему уравнений для отыскания коэффициентов. В качестве частных значений переменной удобнее всего выбирать корни знаменателя (как действительные, так и комплексные). При этом почти все члены в правой части равенства (имеется в виду равенство двух многочленов) обращаются в нуль, что позволяет легко находить оставшиеся коэффициенты. При подстановке комплексных значений следует иметь в виду, что два комплексных числа равны тогда и только тогда, когда равны соответственно их действительные и мнимые части. Поэтому из каждого равенства, содержащего комплексные числа, получаются два уравнения.
После нахождения неопределенных коэффициентов остается вычислить интегралы от полученных простейших дробей. Так как при интегрировании простейших дробей получаются, как мы видели, лишь рациональные функции, арктангенсы и логарифмы, то интеграл от любой рациональной функции выражается через рациональную функцию, арктангенсы и логарифмы .
Пример 3. Вычислим интеграл от правильной рациональной дроби \int\frac{6x+1}{x^2+2x-3}\,dx .
Решение. Разложим знаменатель подынтегральной функции на множители:
x^2+2x-3=(x-1)(x+3).
Выпишем подынтегральную функцию и представим ее в виде суммы простейших дробей:
\frac{6x+1}{x^2+2x-3}= \frac{A}{x-1}+\frac{B}{B+3}\,.
Освободившись в этом равенстве от знаменателей, получим:
6x+1=A\cdot (x+3)+B\cdot (x-1)\,.
Для отыскания коэффициентов воспользуемся методом подстановки частных значений. Для нахождения коэффициента A положим x=1 . Тогда из равенства (2) получим 7=4A , откуда A=7/4 . Для отыскания коэффициента B положим x=-3 . Тогда из равенства (2) получим -17=-4B , откуда B=17/4 .
Итак, \frac{6x+1}{x^2+2x-3}= \frac{7}{4}\cdot\frac{1}{x-1}+ \frac{17}{4}\cdot\frac{1}{x+3} . Значит,
\int\frac{6x+1}{x^2+2x-3}\,dx= \frac{7}{4}\int\frac{dx}{x-1}+ \frac{17}{4}\int\frac{dx}{x+3}= \frac{7}{4}\ln|x-1|+ \frac{17}{4}\ln|x+3|+C.
Пример 4. Вычислим \int\frac{x^4+2x^2+8x+5}{(x^2+2)(x-1)^2(x+2)}\,dx .
Решение. Выпишем подынтегральную функцию и представим ее в виде суммы простейших дробей. В знаменателе содержится множитель x^2+2 , не имеющий действительных корней, ему соответствует дробь 2-го рода: \frac{Ax+B}{x^2+2} множителю (x-1)^2 соответствует сумма двух дробей 1-го рода: \frac{C}{(x-1)^2}+ \frac{D}{x-1} ; наконец, множителю x+2 соответствует одна дробь 1-го рода \frac{E}{x+2} . Таким образом, подынтегральную функцию мы представим в виде суммы четырех дробей:
\frac{x^4+2x^2+8x+5}{(x^2+2)(x-1)^2(x+2)}= \frac{Ax+B}{x^2+2}+ \frac{C}{(x-1)^2}+ \frac{D}{x-1}+ \frac{E}{x+2}\,.
Освободимся в этом равенстве от знаменателей. Получим:
\begin{aligned} x^4+2x^2+8x+5&= (Ax+B)(x-1)^2(x+2)+ C(x^2+2)(x+2)\,+\\ &\phantom{=}+ D(x^2+2)(x-1)(x+2)+ E(x^2+2)(x-1)^2.\end{aligned}
Знаменатель подынтегральной функции имеет два действительных корня: x=1 и x=-2 . При подстановке в равенство (4) значения x=1 получаем 16=9C , откуда находим C=16/9 . При подстановке x=-2 получаем 13=54E и соответственно определяем E=13/54 . Подстановка значения x=i\,\sqrt{2} (корня многочлена x^2+2 ) позволяет перейти к равенству
4-4+8\,i\,\sqrt{2}+5= (A\,i\,\sqrt{2}+B)\cdot (i\,\sqrt{2}-1)^2\cdot (i\,\sqrt{2}+2).
Оно преобразуется к виду:
(10A+2B)+(2A-5B)\sqrt{2}\,i= 5+8\sqrt{2}\,i , откуда 10A+2B=5 , а (2A-5B)\sqrt{2}=8\sqrt{2} .
Решив систему двух уравнений с двумя переменными \begin{cases}10A+2B=5,\\ 2A-5B=8,\end{cases} находим: A=\frac{41}{54},~ B=-\frac{35}{27} .
Осталось определить значение коэффициента D . Для этого в равенстве (4) раскроем скобки, приведем подобные члены, а затем сравним коэффициенты при x^4 . Получим:
A+D+E=1 , то есть D=0 .
Подставим найденные значения коэффициентов в равенство (3):
\frac{x^4+2x^2+8x+5}{(x^2+2)(x-1)^2(x+2)}= \frac{\drac{41}{54}\,x- \dfrac{35}{27}}{x^2+2}+ \frac{16}{9}\frac{1}{(x-1)^2}+ \frac{13}{54}\frac{1}{x+2}\,
а затем перейдем к интегрированию:
\begin{aligned}\int\frac{x^4+2x^2+8x+5}{(x^2+2)(x-1)^2(x+2)}\,dx&= \frac{41}{54}\int\frac{x\,dx}{x^2+2}- \frac{35}{27}\int\frac{dx}{x^2+2}+ \frac{16}{9} \int\frac{dx}{(x-1)^2}+ \frac{13}{54}\int\frac{dx}{x+2}=\\ &=\frac{41}{108}\ln(x^2+2)- \frac{35}{27\sqrt{2}}\operatorname{arctg}\frac{x}{\sqrt{2}}- \frac{16}{9(x-1)}+ \frac{13}{54} \ln|x+2|+C.\end{aligned}
Интегрирование неправильных дробей
Пусть нужно проинтегрировать функцию y=\frac{f(x)}{g(x)} , где f(x) и g(x) - многочлены, причем степень многочлена f(x) больше или равна степени многочлена g(x) . В этом случае прежде всего необходимо выделить целую часть неправильной дроби \frac{f(x)}{g(x)} , т. е. представить ее в виде
\frac{f(x)}{g(x)}=s(x)+ \frac{r(x)}{g(x)}\,
где s(x) - многочлен степени, равной разности степеней многочленов f(x) и g(x) , а \frac{r(x)}{g(x)} - правильная дробь.
Тогда имеем \int\frac{f(x)}{g(x)}\,dx= \int s(x)\,dx+ \int\frac{r(x)}{g(x)}\,dx\,. .
Пример 5. Вычислим интеграл от неправильной дроби \int\frac{x^4-4x^3+x^2+16x-11}{(x-1)(x+2)(x-3)}\,dx .
Решение. Имеем:
\begin{aligned}g(x)&=(x-1)(x+2)(x-3)= x^3-2x^2-5x+6,\\ f(x)&=x^4-4x^3+x^2+16x-11. \end{aligned}
Для выделения целой части разделим f(x) на g(x) : \frac{f(x)}{g(x)}= x-2+\frac{2x^2+1}{x^3-2x^2-5x+6}\,.
Значит, \int\frac{x^4-4x^3+x^2+16x-11}{(x-1)(x+2)(x-3)}\,dx= \int(x-2)dx+ \int\frac{2x^2+1}{(x-1)(x+2)(x-3)}\,dx
Имеем: \int(x-2)dx=\frac{x^2}{2}-2x+C .
Для вычисления интеграла \int\frac{2x^2+1}{(x-1)(x+2)(x-3)}\,dx применяется, как и выше, метод неопределенных коэффициентов. После вычислений, которые мы оставляем читателю, получаем.
Рациональная функция - это дробь вида , числитель и знаменатель которой - многочлены или произведения многочленов.
Пример 1. Шаг 2.
.
Умножаем неопределённые коэффициенты на многочлены, которых нет в данной отдельной дроби, но которые есть в других полученных дробях:
Раскрываем скобки и приравниваем полученое к полученному выражению числитель исходной подынтегральной дроби:
В обеих частях равенства отыскиваем слагаемые с одинаковыми степенями икса и составляем из них систему уравнений:
.
Сокращаем все иксы и получаем эквивалентную систему уравнений:
.
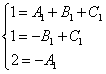Таким образом, окончательное разложение подынтегральной дроби на сумму простых дробей:
.
Пример 2. Шаг 2. На шаге 1 получили следующее разложение исходной дроби на сумму простых дробей с неопределёнными коэффициентами в числителях:
.
Теперь начинаем искать неопределённые коэффициенты. Для этого числитель исходной дроби в выражении функции приравниваем к числителю выражения, полученного после приведения суммы дробей к общему знаменателю:
Теперь требуется составить и решить систему уравнений. Для этого приравниваем коэффициенты при переменной в соответствующей степени в числителе исходного выражения функции и аналогичные коэффициенты в полученном на предыдущем шаге выражения:
Решаем полученную систему:
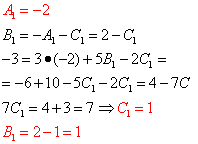
Итак, , отсюда
.
Пример 3. Шаг 2. На шаге 1 получили следующее разложение исходной дроби на сумму простых дробей с неопределёнными коэффициентами в числителях:
Начинаем искать неопределённые коэффициенты. Для этого числитель исходной дроби в выражении функции приравниваем к числителю выражения, полученного после приведения суммы дробей к общему знаменателю:
Как и в предыдущих примерах составляем систему уравнений:
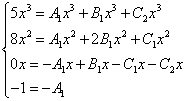
Сокращаем иксы и получаем эквивалентную систему уравнений:
Решая систему, получаем следующие значения неопределённых коэффициентов:
Получаем окончательное разложение подынтегральной дроби на сумму простых дробей:
.
Пример 4. Шаг 2. На шаге 1 получили следующее разложение исходной дроби на сумму простых дробей с неопределёнными коэффициентами в числителях:
.
Как приравнивать числитель исходной дроби к выражению в числителе, полученному после разложения дроби на сумму простых дробей и приведения этой суммы к общему знаменателю, мы уже знаем из предыдуших примеров. Поэтому лишь для контроля приведём получившуюся систему уравнений:
Решая систему, получаем следующие значения неопределённых коэффициентов:
Получаем окончательное разложение подынтегральной дроби на сумму простых дробей:
Пример 5. Шаг 2. На шаге 1 получили следующее разложение исходной дроби на сумму простых дробей с неопределёнными коэффициентами в числителях:
.
Самостоятельно приводим к общему знаменателю эту сумму, приравнивать числитель этого выражения к числителю исходной дроби. В результате должна получиться следующая система уравнений:
Решая систему, получаем следующие значения неопределённых коэффициентов:
.
Получаем окончательное разложение подынтегральной дроби на сумму простых дробей:
.
Пример 6. Шаг 2. На шаге 1 получили следующее разложение исходной дроби на сумму простых дробей с неопределёнными коэффициентами в числителях:
Производим с этой суммой те же действия, что и в предыдущих примерах. В результате должна получиться следующая система уравнений:
Решая систему, получаем следующие значения неопределённых коэффициентов:
.
Получаем окончательное разложение подынтегральной дроби на сумму простых дробей:
.
Пример 7. Шаг 2. На шаге 1 получили следующее разложение исходной дроби на сумму простых дробей с неопределёнными коэффициентами в числителях:
.
После известных действий с полученной суммой должна получиться следующая система уравнений:
Решая систему, получаем следующие значения неопределённых коэффициентов:
Получаем окончательное разложение подынтегральной дроби на сумму простых дробей:
.
Пример 8. Шаг 2. На шаге 1 получили следующее разложение исходной дроби на сумму простых дробей с неопределёнными коэффициентами в числителях:
.
Внесём некоторые изменения в уже доведённые до автоматизма действия для получения системы уравнений. Есть искусственный приём, который в некоторых случаях помогает избежать лишних вычислений. Приводя сумму дробей к общему знаменателю получаем и приравнивая числитель этого выражения к числителю исходной дроби, получаем.
Интегрирование рациональных функций Дробно – рациональная функция Простейшие рациональные дроби Разложение рациональной дроби на простейшие дроби Интегрирование простейших дробей Общее правило интегрирования рациональных дробей
многочлен степени n. Дробно – рациональная функция Дробно – рациональной функцией называется функция, равная отношению двух многочленов: Рациональная дробь называется правильной, если степень числителя меньше степени знаменателя, то есть m < n , в противном случае дробь называется неправильной. многочлен степени m Всякую неправильную рациональную дробь можно, путем деления числителя на знаменатель, представить в виде суммы многочлена L(x) и правильной рациональной дроби:)()()(x. Q x. P xf n m)()()(x. Q x. R x. L x. Q x. P
Дробно – рациональная функция Привести неправильную дробь к правильному виду: 2 95 4 x xx 95 4 xx 2 x 3 x 34 2 xx 952 3 xx 2 2 x 23 42 xx 954 2 xx x 4 xx 84 2 93 x 3 63 x 15 2 95 4 x xx 342 23 xxx 2 15 x
Простейшие рациональные дроби Правильные рациональные дроби вида: Называются простейшими рациональными дробями типов. ax A); 2(Nkk ax A k)04(2 2 qp qpxx NMx); 2; 04(2 2 Nkkqp qpxx NMx k V V,
Разложение рациональной дроби на простейшие дроби Теорема: Всякую правильную рациональную дробь, знаменатель которой разложен на множители: можно представить, притом единственным образом в виде суммы простейших дробей: s k qxpxxxxxx. Q)()()(22 2 11 2 21)()(x. Q x. P 1 xx A k k xx B)()(2 2 2 1 11 2 qxpx DCx 2 22 22 2 11)(qxpx Nx. M s ss qxpx Nx. M)(
Разложение рациональной дроби на простейшие дроби Поясним формулировку теоремы на следующих примерах: Для нахождения неопределенных коэффициентов A, B, C, D … применяют два метода: метод сравнивания коэффициентов и метод частных значений переменной. Первый метод рассмотрим на примере. 3 2)3)(2(4 xx x 2 x A 3 3 2 21)3()3(3 x B x B 1 2 x DCx 22 22 2 11)1(1 xx Nx. M)1(3 22 3 xx x 2 21 x A 22 2)1)(4(987 xxx xx 4 x
Разложение рациональной дроби на простейшие дроби Представить дробь в виде суммы простейших дробей: Приведем простейшие дроби к общему знаменателю Приравняем числители получившейся и исходной дробей Приравняем коэффициенты при одинаковых степенях х)52)(1(332 2 2 xxx xx 1 x A 52 2 xx CBx)52)(1()1)(()52(2 2 xxx x. CBxxx. A 33252 222 xx. CBx. Cx. Bx. AAx. Ax 35 32 2 0 1 2 CAx BAx 2 3 1 C B A 52 23 1 1 2 xx x x
Интегрирование простейших дробей Найдем интегралы от простейших рациональных дробей: Интегрирование дроби 3 типа рассмотрим на примере. dx ax A k dx qpxx NMx 2 ax axd A)(Cax. Aln)(axdax. A k C k ax. A k
Интегрирование простейших дробейdx xx x 102 13 2 dx xx x 9)12(13 2 dx x x 9)1(13 2 dtdx tx tx 1 1 dt t t 9 1)1(3 2 dt t t 9 23 2 9 322 t dtt 9 9 2 3 2 2 t td 33 2 t arctg. C t arctgt 33 2 9 ln 2 32 C x arctgxx 3 1 3 2 102 ln
Интегрирование простейших дробей Интеграл данного типа с помощью подстановки: приводится к сумме двух интегралов: Первый интеграл вычисляется методом внесения t под знак дифференциала. Второй интеграл вычисляется с помощью рекуррентной формулы: dx qpxx NMx k 2 V t p x 2 kk at dt N at dtt M 22122 1221222))(1(222 321 kkkk atk t k k aat dt
Интегрирование простейших дробей a = 1; k = 3 323)1(t dt tarctg t dt 1 21)1)(12(2222 322 1 21222 t t t dt)1(22 1 2 t t tarctg 2223)1)(13(2232 332 t t C t t tarctg 222)1(4)1(
Общее правило интегрирования рациональных дробей Если дробь неправильная, то представить ее в виде суммы многочлена и правильной дроби. Разложив знаменатель правильной рациональной дроби на множители, представить ее в виде суммы простейших дробей с неопределенными коэффициентами Найти неопределенные коэффициенты методом сравнения коэффициентов или методом частных значений переменной. Проинтегрировать многочлен и полученную сумму простейших дробей.
Пример Приведем дробь к правильному виду. dx xxx 23 35 2 442 35 xxxxxx 23 2 2 x 345 2 xxx 442 34 xxx x 2 234 242 xxx 4425 23 xxx xxx 23 35 2 442 xxx xx xx 23 2 2 2 48 52 5 xxx 5105 23 48 2 xx
Пример Разложим знаменатель правильной дроби на множители Представим дробь в виде суммы простейших дробей Найдем неопределенные коэффициенты методом частных значений переменной xxx xx 23 2 2 48 2 2)1(48 xx xx 2)1(1 x C x B x A 2 2)1()1(xx Cxx. Bxx. A 48)1()1(22 xx. Cxx. Bxx. A 5241 31 40 CBAx Cx Ax 3 12 4 C B A xxx xx 23 2 2 48 2)1(3 1 124 xxx
Пример dx xx 2 2)1(3 1 124 52 2 2)1(3 1 12452 x dx dxxdxdxx C x xxxx x 1 3 1 ln 12 ln
Материал, изложенный в этой теме, опирается на сведения, представленные в теме "Рациональные дроби. Разложение рациональных дробей на элементарные (простейшие) дроби" . Очень советую хотя бы бегло просмотреть эту тему перед тем, как переходить к чтению данного материала. Кроме того, нам будет нужна таблица неопределенных интегралов .
Напомню пару терминов. О их шла речь в соответствующей теме , посему тут ограничусь краткой формулировкой.
Отношение двух многочленов $\frac{P_n(x)}{Q_m(x)}$ называется рациональной функцией или рациональной дробью. Рациональная дробь называется правильной , если $n < m$, т.е. если степень многочлена, стоящего в числителе, меньше степени многочлена, стоящего в знаменателе. В противном случае (если $n ≥ m$) дробь называется неправильной .
Элементарными (простейшими) рациональными дробями именуют рациональные дроби четырёх типов:
- $\frac{A}{x-a}$;
- $\frac{A}{(x-a)^n}$ ($n=2,3,4, \ldots$);
- $\frac{Mx+N}{x^2+px+q}$ ($p^2-4q < 0$);
- $\frac{Mx+N}{(x^2+px+q)^n}$ ($p^2-4q < 0$; $n=2,3,4,\ldots$).
Примечание (желательное для более полного понимания текста): показать\скрыть
Зачем нужно условие $p^2-4q < 0$ в дробях третьего и четвертого типов? Рассмотрим квадратное уравнение $x^2+px+q=0$. Дискриминант этого уравнения $D=p^2-4q$. По сути, условие $p^2-4q < 0$ означает, что $D < 0$. Если $D < 0$, то уравнение $x^2+px+q=0$ не имеет действительных корней. Т.е. выражение $x^2+px+q$ неразложимо на множители. Именно эта неразложимость нас и интересует.
Например, для выражения $x^2+5x+10$ получим: $p^2-4q=5^2-4\cdot 10=-15$. Так как $p^2-4q=-15 < 0$, то выражение $x^2+5x+10$ нельзя разложить на множители.
Кстати сказать, для этой проверки вовсе не обязательно, чтобы коэффициент перед $x^2$ равнялся 1. Например, для $5x^2+7x-3=0$ получим: $D=7^2-4\cdot 5 \cdot (-3)=109$. Так как $D > 0$, то выражение $5x^2+7x-3$ разложимо на множители.
Примеры рациональных дробей (правильных и неправильных), а также примеры разложения рациональной дроби на элементарные можно найти . Здесь нас будут интересовать лишь вопросы их интегрирования. Начнём с интегрирования элементарных дробей. Итак, каждый из четырёх типов указанных выше элементарных дробей несложно проинтегрировать, используя формулы, указанные ниже. Напомню, что при интегрировании дробей типа (2) и (4) предполагается $n=2,3,4,\ldots$. Формулы (3) и (4) требуют выполнение условия $p^2-4q < 0$.
\begin{equation} \int \frac{A}{x-a} dx=A\cdot \ln |x-a|+C \end{equation} \begin{equation} \int\frac{A}{(x-a)^n}dx=-\frac{A}{(n-1)(x-a)^{n-1}}+C \end{equation} \begin{equation} \int \frac{Mx+N}{x^2+px+q} dx= \frac{M}{2}\cdot \ln (x^2+px+q)+\frac{2N-Mp}{\sqrt{4q-p^2}}\arctg\frac{2x+p}{\sqrt{4q-p^2}}+C \end{equation}
Для $\int\frac{Mx+N}{(x^2+px+q)^n}dx$ делается замена $t=x+\frac{p}{2}$, после полученный интерал разбивается на два. Первый будет вычисляться с помощью внесения под знак дифференциала, а второй будет иметь вид $I_n=\int\frac{dt}{(t^2+a^2)^n}$. Этот интеграл берётся с помощью рекуррентного соотношения
\begin{equation} I_{n+1}=\frac{1}{2na^2}\frac{t}{(t^2+a^2)^n}+\frac{2n-1}{2na^2}I_n, \; n\in N \end{equation}
Вычисление такого интеграла разобрано в примере №7 (см. третью часть).
Схема вычисления интегралов от рациональных функций (рациональных дробей):
- Если подынтегральная дробь является элементарной, то применить формулы (1)-(4).
- Если подынтегральная дробь не является элементарной, то представить её в виде суммы элементарных дробей, а затем проинтегрировать, используя формулы (1)-(4).
Указанный выше алгоритм интегрирования рациональных дробей имеет неоспоримое достоинство - он универсален. Т.е. пользуясь этим алгоритмом можно проинтегрировать любую рациональную дробь. Именно поэтому почти все замены переменных в неопределённом интеграле (подстановки Эйлера, Чебышева, универсальная тригонометрическая подстановка) делаются с таким расчётом, чтобы после оной замены получить под интералом рациональную дробь. А к ней уже применить алгоритм. Непосредственное применение этого алгоритма разберём на примерах, предварительно сделав небольшое примечание.
$$ \int\frac{7dx}{x+9}=7\ln|x+9|+C. $$
В принципе, этот интеграл несложно получить без механического применения формулы . Если вынести константу $7$ за знак интеграла и учесть, что $dx=d(x+9)$, то получим:
$$ \int\frac{7dx}{x+9}=7\cdot \int\frac{dx}{x+9}=7\cdot \int\frac{d(x+9)}{x+9}=|u=x+9|=7\cdot\int\frac{du}{u}=7\ln|u|+C=7\ln|x+9|+C. $$
Для детальной информации рекомедую посмотреть тему . Там подробно поясняется, как решаются подобные интегралы. Кстати, формула доказывается теми же преобразованиями, что были применены в этом пункте при решении "вручную".
2) Вновь есть два пути: применить готовую формулу или обойтись без неё. Если применять формулу , то следует учесть, что коэффициент перед $x$ (число 4) придется убрать. Для этого оную четвёрку просто вынесем за скобки:
$$ \int\frac{11dx}{(4x+19)^8}=\int\frac{11dx}{\left(4\left(x+\frac{19}{4}\right)\right)^8}= \int\frac{11dx}{4^8\left(x+\frac{19}{4}\right)^8}=\int\frac{\frac{11}{4^8}dx}{\left(x+\frac{19}{4}\right)^8}. $$
Теперь настал черёд и для применения формулы :
$$ \int\frac{\frac{11}{4^8}dx}{\left(x+\frac{19}{4}\right)^8}=-\frac{\frac{11}{4^8}}{(8-1)\left(x+\frac{19}{4} \right)^{8-1}}+C= -\frac{\frac{11}{4^8}}{7\left(x+\frac{19}{4} \right)^7}+C=-\frac{11}{7\cdot 4^8 \left(x+\frac{19}{4} \right)^7}+C. $$
Можно обойтись и без применения формулы . И даже без вынесения константы $4$ за скобки. Если учесть, что $dx=\frac{1}{4}d(4x+19)$, то получим:
$$ \int\frac{11dx}{(4x+19)^8}=11\int\frac{dx}{(4x+19)^8}=\frac{11}{4}\int\frac{d(4x+19)}{(4x+19)^8}=|u=4x+19|=\\ =\frac{11}{4}\int\frac{du}{u^8}=\frac{11}{4}\int u^{-8}\;du=\frac{11}{4}\cdot\frac{u^{-8+1}}{-8+1}+C=\\ =\frac{11}{4}\cdot\frac{u^{-7}}{-7}+C=-\frac{11}{28}\cdot\frac{1}{u^7}+C=-\frac{11}{28(4x+19)^7}+C. $$
Подробные пояснения по нахождению подобных интегралов даны в теме "Интегрирование подстановкой (внесение под знак дифференциала)" .
3) Нам нужно проинтегрировать дробь $\frac{4x+7}{x^2+10x+34}$. Эта дробь имеет структуру $\frac{Mx+N}{x^2+px+q}$, где $M=4$, $N=7$, $p=10$, $q=34$. Однако чтобы убедиться, что это действительно элементарная дробь третьего типа, нужно проверить выполнение условия $p^2-4q < 0$. Так как $p^2-4q=10^2-4\cdot 34=-16 < 0$, то мы действительно имеем дело с интегрированием элементарной дроби третьего типа. Как и в предыдущих пунктах есть два пути для нахождения $\int\frac{4x+7}{x^2+10x+34}dx$. Первый путь - банально использовать формулу . Подставив в неё $M=4$, $N=7$, $p=10$, $q=34$ получим:
$$ \int\frac{4x+7}{x^2+10x+34}dx = \frac{4}{2}\cdot \ln (x^2+10x+34)+\frac{2\cdot 7-4\cdot 10}{\sqrt{4\cdot 34-10^2}} \arctg\frac{2x+10}{\sqrt{4\cdot 34-10^2}}+C=\\ =2\cdot \ln (x^2+10x+34)+\frac{-26}{\sqrt{36}} \arctg\frac{2x+10}{\sqrt{36}}+C =2\cdot \ln (x^2+10x+34)+\frac{-26}{6} \arctg\frac{2x+10}{6}+C=\\ =2\cdot \ln (x^2+10x+34)-\frac{13}{3} \arctg\frac{x+5}{3}+C. $$
Решим этот же пример, но без использования готовой формулы. Попробуем выделить в числителе производную знаменателя. Что это означает? Мы знаем, что $(x^2+10x+34)"=2x+10$. Именно выражение $2x+10$ нам и предстоит вычленить в числителе. Пока что числитель содержит лишь $4x+7$, но это ненадолго. Применим к числителю такое преобразование:
$$ 4x+7=2\cdot 2x+7=2\cdot (2x+10-10)+7=2\cdot(2x+10)-2\cdot 10+7=2\cdot(2x+10)-13. $$
Теперь в числителе появилось требуемое выражение $2x+10$. И наш интеграл можно переписать в таком виде:
$$ \int\frac{4x+7}{x^2+10x+34} dx= \int\frac{2\cdot(2x+10)-13}{x^2+10x+34}dx. $$
Разобьём подынтегральную дробь на две. Ну и, соответственно, сам интеграл тоже "раздвоим":
$$ \int\frac{2\cdot(2x+10)-13}{x^2+10x+34}dx=\int \left(\frac{2\cdot(2x+10)}{x^2+10x+34}-\frac{13}{x^2+10x+34} \right)\; dx=\\ =\int \frac{2\cdot(2x+10)}{x^2+10x+34}dx-\int\frac{13dx}{x^2+10x+34}=2\cdot\int \frac{(2x+10)dx}{x^2+10x+34}-13\cdot\int\frac{dx}{x^2+10x+34}. $$
Поговорим сперва про первый интеграл, т.е. про $\int \frac{(2x+10)dx}{x^2+10x+34}$. Так как $d(x^2+10x+34)=(x^2+10x+34)"dx=(2x+10)dx$, то в числителе подынтегральной дроби расположен дифференциал знаменателя. Короче говоря, вместо выражения $(2x+10)dx$ запишем $d(x^2+10x+34)$.
Теперь скажем пару слов и о втором интеграле. Выделим в знаменателе полный квадрат: $x^2+10x+34=(x+5)^2+9$. Кроме того, учтём $dx=d(x+5)$. Теперь полученную нами ранее сумму интегралов можно переписать в несколько ином виде:
$$ 2\cdot\int \frac{(2x+10)dx}{x^2+10x+34}-13\cdot\int\frac{dx}{x^2+10x+34} =2\cdot\int \frac{d(x^2+10x+34)}{x^2+10x+34}-13\cdot\int\frac{d(x+5)}{(x+5)^2+9}. $$
Если в первом интеграле сделать замену $u=x^2+10x+34$, то он примет вид $\int\frac{du}{u}$ и возьмётся простым применением второй формулы из . Что же касается второго интеграла, то для него осуществима замена $u=x+5$, после которой он примет вид $\int\frac{du}{u^2+9}$. Это чистейшей воды одиннадцатая формула из таблицы неопределенных интегралов . Итак, возвращаясь к сумме интегралов, будем иметь:
$$ 2\cdot\int \frac{d(x^2+10x+34)}{x^2+10x+34}-13\cdot\int\frac{d(x+5)}{(x+5)^2+9} =2\cdot\ln(x^2+10x+34)-\frac{13}{3}\arctg\frac{x+5}{3}+C. $$
Мы получили тот же ответ, что и при применении формулы , что, собственно говоря, неудивительно. Вообще, формула доказывается теми же методами, кои мы применяли для нахождения данного интеграла. Полагаю, что у внимательного читателя тут может возникнуть один вопрос, посему сформулирую его:
Вопрос №1
Если к интегралу $\int \frac{d(x^2+10x+34)}{x^2+10x+34}$ применять вторую формулу из таблицы неопределенных интегралов , то мы получим следующее:
$$ \int \frac{d(x^2+10x+34)}{x^2+10x+34}=|u=x^2+10x+34|=\int\frac{du}{u}=\ln|u|+C=\ln|x^2+10x+34|+C. $$
Почему же в решении отсутствовал модуль?
Ответ на вопрос №1
Вопрос совершенно закономерный. Модуль отсутствовал лишь потому, что выражение $x^2+10x+34$ при любом $x\in R$ больше нуля. Это совершенно несложно показать несколькими путями. Например, так как $x^2+10x+34=(x+5)^2+9$ и $(x+5)^2 ≥ 0$, то $(x+5)^2+9 > 0$. Можно рассудить и по-иному, не привлекая выделение полного квадрата. Так как $10^2-4\cdot 34=-16 < 0$, то $x^2+10x+34 > 0$ при любом $x\in R$ (если эта логическая цепочка вызывает удивление, советую посмотреть графический метод решения квадратных неравенств). В любом случае, так как $x^2+10x+34 > 0$, то $|x^2+10x+34|=x^2+10x+34$, т.е. вместо модуля можно использовать обычные скобки.
Все пункты примера №1 решены, осталось лишь записать ответ.
Ответ :
- $\int\frac{7dx}{x+9}=7\ln|x+9|+C$;
- $\int\frac{11dx}{(4x+19)^8}=-\frac{11}{28(4x+19)^7}+C$;
- $\int\frac{4x+7}{x^2+10x+34}dx=2\cdot\ln(x^2+10x+34)-\frac{13}{3}\arctg\frac{x+5}{3}+C$.
Пример №2
Найти интеграл $\int\frac{7x+12}{3x^2-5x-2}dx$.
На первый взгляд подынтегральая дробь $\frac{7x+12}{3x^2-5x-2}$ очень похожа на элементарную дробь третьего типа, т.е. на $\frac{Mx+N}{x^2+px+q}$. Кажется, что единcтвенное отличие - это коэффициент $3$ перед $x^2$, но ведь коэффициент и убрать недолго (за скобки вынести). Однако это сходство кажущееся. Для дроби $\frac{Mx+N}{x^2+px+q}$ обязательным является условие $p^2-4q < 0$, которое гарантирует, что знаменатель $x^2+px+q$ нельзя разложить на множители. Проверим, как обстоит дело с разложением на множители у знаменателя нашей дроби, т.е. у многочлена $3x^2-5x-2$.
У нас коэффициент перед $x^2$ не равен единице, посему проверить условие $p^2-4q < 0$ напрямую мы не можем. Однако тут нужно вспомнить, откуда взялось выражение $p^2-4q$. Это всего лишь дискриминант квадратного уравнения $x^2+px+q=0$. Если дискриминант меньше нуля, то выражение $x^2+px+q$ на множители не разложишь. Вычислим дискриминант многочлена $3x^2-5x-2$, расположенного в знаменателе нашей дроби: $D=(-5)^2-4\cdot 3\cdot(-2)=49$. Итак, $D > 0$, посему выражение $3x^2-5x-2$ можно разложить на множители. А это означает, что дробь $\frac{7x+12}{3x^2-5x-2}$ не является элементаной дробью третьего типа, и применять к интегралу $\int\frac{7x+12}{3x^2-5x-2}dx$ формулу нельзя.
Ну что же, если заданная рациональная дробь не является элементарной, то её нужно представить в виде суммы элементарных дробей, а затем проинтегрировать. Короче говоря, след воспользоваться . Как разложить рациональную дробь на элементарные подробно написано . Начнём с того, что разложим на множители знаменатель:
$$ 3x^2-5x-2=0;\\ \begin{aligned} & D=(-5)^2-4\cdot 3\cdot(-2)=49;\\ & x_1=\frac{-(-5)-\sqrt{49}}{2\cdot 3}=\frac{5-7}{6}=\frac{-2}{6}=-\frac{1}{3};\\ & x_2=\frac{-(-5)+\sqrt{49}}{2\cdot 3}=\frac{5+7}{6}=\frac{12}{6}=2.\\ \end{aligned}\\ 3x^2-5x-2=3\cdot\left(x-\left(-\frac{1}{3}\right)\right)\cdot (x-2)=3\cdot\left(x+\frac{1}{3}\right)(x-2). $$
Подынтеральную дробь представим в таком виде:
$$ \frac{7x+12}{3x^2-5x-2}=\frac{7x+12}{3\cdot\left(x+\frac{1}{3}\right)(x-2)}=\frac{\frac{7}{3}x+4}{\left(x+\frac{1}{3}\right)(x-2)}. $$
Теперь разложим дробь $\frac{\frac{7}{3}x+4}{\left(x+\frac{1}{3}\right)(x-2)}$ на элементарные:
$$ \frac{\frac{7}{3}x+4}{\left(x+\frac{1}{3}\right)(x-2)} =\frac{A}{x+\frac{1}{3}}+\frac{B}{x-2}=\frac{A(x-2)+B\left(x+\frac{1}{3}\right)}{\left(x+\frac{1}{3}\right)(x-2)};\\ \frac{7}{3}x+4=A(x-2)+B\left(x+\frac{1}{3}\right). $$
Чтобы найти коэффициенты $A$ и $B$ есть два стандартных пути: метод неопределённых коэффициентов и метод подстановки частных значений. Применим метод подстановки частных значений, подставляя $x=2$, а затем $x=-\frac{1}{3}$:
$$ \frac{7}{3}x+4=A(x-2)+B\left(x+\frac{1}{3}\right).\\ x=2;\; \frac{7}{3}\cdot 2+4=A(2-2)+B\left(2+\frac{1}{3}\right); \; \frac{26}{3}=\frac{7}{3}B;\; B=\frac{26}{7}.\\ x=-\frac{1}{3};\; \frac{7}{3}\cdot \left(-\frac{1}{3} \right)+4=A\left(-\frac{1}{3}-2\right)+B\left(-\frac{1}{3}+\frac{1}{3}\right); \; \frac{29}{9}=-\frac{7}{3}A;\; A=-\frac{29\cdot 3}{9\cdot 7}=-\frac{29}{21}.\\ $$
Так как коэффициенты найдены, осталось лишь записать готовое разложение:
$$ \frac{\frac{7}{3}x+4}{\left(x+\frac{1}{3}\right)(x-2)}=\frac{-\frac{29}{21}}{x+\frac{1}{3}}+\frac{\frac{26}{7}}{x-2}. $$
В принципе, можно такую запись оставить, но мне по душе более аккуратный вариант:
$$ \frac{\frac{7}{3}x+4}{\left(x+\frac{1}{3}\right)(x-2)}=-\frac{29}{21}\cdot\frac{1}{x+\frac{1}{3}}+\frac{26}{7}\cdot\frac{1}{x-2}. $$
Возвращаясь к исходному интегралу, подставим в него полученное разложение. Затем разобьём интеграл на два, и к каждому применим формулу . Константы я предпочитаю сразу выносить за знак интеграла:
$$ \int\frac{7x+12}{3x^2-5x-2}dx =\int\left(-\frac{29}{21}\cdot\frac{1}{x+\frac{1}{3}}+\frac{26}{7}\cdot\frac{1}{x-2}\right)dx=\\ =\int\left(-\frac{29}{21}\cdot\frac{1}{x+\frac{1}{3}}\right)dx+\int\left(\frac{26}{7}\cdot\frac{1}{x-2}\right)dx =-\frac{29}{21}\cdot\int\frac{dx}{x+\frac{1}{3}}+\frac{26}{7}\cdot\int\frac{dx}{x-2}dx=\\ =-\frac{29}{21}\cdot\ln\left|x+\frac{1}{3}\right|+\frac{26}{7}\cdot\ln|x-2|+C. $$
Ответ : $\int\frac{7x+12}{3x^2-5x-2}dx=-\frac{29}{21}\cdot\ln\left|x+\frac{1}{3}\right|+\frac{26}{7}\cdot\ln|x-2|+C$.
Пример №3
Найти интеграл $\int\frac{x^2-38x+157}{(x-1)(x+4)(x-9)}dx$.
Нам нужно проинтегрировать дробь $\frac{x^2-38x+157}{(x-1)(x+4)(x-9)}$. В числителе расположен многочлен второй степени, а в знаменателе - многочлен третьей степени. Так как степень многочлена в числителе меньше степени многочлена в знаменателе, т.е. $2 < 3$, то подынтегральная дробь является правильной. Разложение этой дроби на элементарные (простейшие) было получено в примере №3 на странице, посвящённой разложению рациональных дробей на элементарные. Полученное разложение таково:
$$ \frac{x^2-38x+157}{(x-1)(x+4)(x-9)}=-\frac{3}{x-1}+\frac{5}{x+4}-\frac{1}{x-9}. $$
Нам останется только разбить заданный интеграл на три, и к каждому применить формулу . Константы я предпочитаю сразу выносить за знак интеграла:
$$ \int\frac{x^2-38x+157}{(x-1)(x+4)(x-9)}dx=\int\left(-\frac{3}{x-1}+\frac{5}{x+4}-\frac{1}{x-9} \right)dx=\\=-3\cdot\int\frac{dx}{x-1}+ 5\cdot\int\frac{dx}{x+4}-\int\frac{dx}{x-9}=-3\ln|x-1|+5\ln|x+4|-\ln|x-9|+C. $$
Ответ : $\int\frac{x^2-38x+157}{(x-1)(x+4)(x-9)}dx=-3\ln|x-1|+5\ln|x+4|-\ln|x-9|+C$.
Продолжение разбора примеров этой темы расположено во второй части.
