Математическое ожидание. Математическим ожиданием дискретной случайной величины Х , принимающей конечное число значений х i с вероятностями р i , называется сумма:
Математическим ожиданием непрерывной случайной величины Х называется интеграл от произведения ее значений х на плотность распределения вероятностей f (x ):
 (6б
)
(6б
)
Несобственный интеграл (6б ) предполагается абсолютно сходящимся (в противном случае говорят, что математическое ожидание М (Х ) не существует). Математическое ожидание характеризует среднее значение случайной величины Х . Его размерность совпадает с размерностью случайной величины.
Свойства математического ожидания:
Дисперсия. Дисперсией случайной величины Х называется число:
Дисперсия является характеристикой рассеяния значений случайной величины Х относительно ее среднего значения М (Х ). Размерность дисперсии равна размерности случайной величины в квадрате. Исходя из определений дисперсии (8) и математического ожидания (5) для дискретной случайной величины и (6) для непрерывной случайной величины получим аналогичные выражения для дисперсии:
 (9)
(9)
Здесь m = М (Х ).
Свойства дисперсии:
Среднее квадратичное отклонение:
![]() (11)
(11)
Так как размерность среднего квадратичного отклонения та же, что и у случайной величины, оно чаще, чем дисперсия, используется как мера рассеяния.
Моменты распределения. Понятия математического ожидания и дисперсии являются частными случаями более общего понятия для числовых характеристик случайных величин – моментов распределения . Моменты распределения случайной величины вводятся как математические ожидания некоторых простейших функций от случайной величины. Так, моментом порядка k относительно точки х 0 называется математическое ожидание М (Х – х 0 )k . Моменты относительно начала координат х = 0 называются начальными моментами и обозначаются:
![]() (12)
(12)
Начальный момент первого порядка есть центр распределения рассматриваемой случайной величины:
![]() (13)
(13)
Моменты относительно центра распределения х = m называются центральными моментами и обозначаются:
![]() (14)
(14)
Из (7) следует, что центральный момент первого порядка всегда равен нулю:
Центральные моменты не зависят от начала отсчета значений случайной величины, так как при сдвиге на постоянное значение С
ее центр распределения сдвигается на то же значение С
, а отклонение от центра не меняется: Х
– m
= (Х
– С
) – (m
– С
).
Теперь очевидно, что дисперсия
– это центральный момент второго порядка
:
Асимметрия. Центральный момент третьего порядка:
![]() (17)
(17)
служит для оценки асимметрии распределения . Если распределение симметрично относительно точки х = m , то центральный момент третьего порядка будет равен нулю (как и все центральные моменты нечетных порядков). Поэтому, если центральный момент третьего порядка отличен от нуля, то распределение не может быть симметричным. Величину асимметрии оценивают с помощью безразмерного коэффициента асимметрии :
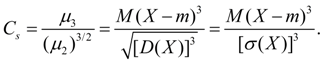 (18)
(18)
Знак коэффициента асимметрии (18) указывает на правостороннюю или левостороннюю асимметрию (рис. 2).

Рис. 2. Виды асимметрии распределений.
Эксцесс. Центральный момент четвертого порядка:
![]() (19)
(19)
служит для оценки так называемого эксцесса , определяющего степень крутости (островершинности) кривой распределения вблизи центра распределения по отношению к кривой нормального распределения. Так как для нормального распределения, то в качестве эксцесса принимается величина:
 (20)
(20)
На рис. 3 приведены примеры кривых распределения с различными значениями эксцесса. Для нормального распределения Е = 0. Кривые, более островершинные, чем нормальная, имеют положительный эксцесс, более плосковершинные – отрицательный.

Рис. 3. Кривые распределения с различной степенью крутости (эксцессом).
Моменты более высоких порядков в инженерных приложениях математической статистики обычно не применяются.
Мода
дискретной
случайной величины – это ее наиболее вероятное значение. Модой
непрерывной
случайной величиныназывается ее значение, при котором плотность вероятности максимальна (рис. 2). Если кривая распределения имеет один максимум, то распределение называется унимодальным
. Если кривая распределения имеет более одного максимума, то распределение называется полимодальным
. Иногда встречаются распределения, кривые которых имеют не максимум, а минимум. Такие распределения называются антимодальными
. В общем случае мода и математическое ожидание случайной величины не совпадают. В частном случае, для модального
, т.е. имеющего моду, симметричного распределения и при условии, что существует математическое ожидание, последнее совпадает с модой и центром симметрии распределения.
Медиана случайной величины Х – это ее значение Ме , для которого имеет место равенство: т.е. равновероятно, что случайная величина Х окажется меньше или больше Ме . Геометрически медиана – это абсцисса точки, в которой площадь под кривой распределения делится пополам (рис. 2). В случае симметричного модального распределения медиана, мода и математическое ожидание совпадают.
Рассмотрим дискретную случайную величину , заданную законом распределения:
Математическое ожидание равно:
Видим, что значительно больше . Это можно объяснить тем, что значение x = –150, намного отличающееся от остальных значений, при возведении в квадрат резко возросло; вероятность же этого значения мала (0,02). Таким образом, переход от M(X) к M(X 2) позволил лучше учесть влияние на математическое ожидание таких значений случайной величины, которые велики по абсолютной величине, но вероятность их появления мала. Разумеется, если бы величина имела несколько больших и маловероятных значений, то переход к величине X 2 , а тем более к величинам , и т.д., позволил бы еще больше «усилить роль» этих больших, но маловероятных возможных значений. Вот почему оказывается целесообразным рассматривать математическое ожидание целой положительной степени случайной величины, причем не только дискретной, но и непрерывной.
Определение 6.10. Начальным моментом го порядка случайной величины называется математическое ожидание величины :
В частности:
Пользуясь этими моментами, формулу для вычисления дисперсии можно записать иначе
Кроме моментов случайной величины целесообразно рассматривать моменты отклонения .
Определение 6.11. Центральным моментом ого порядка случайной величины называется математическое ожидание величины .
![]() (6.23)
(6.23)
В частности,
Легко выводятся соотношения, связывающие начальные и центральные моменты. Так, сравнивая (6.22) и (6.24), получим:
Нетрудно доказать и следующие соотношения:
Аналогично:
Моменты более высоких порядков используются редко. В определении центральных моментов используются отклонения случайной величины от ее математического ожидания (центра). Поэтому моменты называются центральными .
В определении начальных моментов также используются отклонения случайной величины, но не от математического ожидания, а от точки, абсцисса которой равна нулю, являющейся началом координат. Поэтому моменты называются начальными .
В случае непрерывной случайной величины начальный момент го порядка вычисляется по формуле:
![]() (6.27)
(6.27)
Центральный момент го порядка непрерывной случайной величины вычисляется по формуле:
![]() (6.28)
(6.28)
Предположим, что распределение случайной величины симметрично относительно математического ожидания. Тогда все центральные моменты нечетного порядка равны нулю. Это можно объяснить тем, что для каждого положительного значения величины X-M(X) найдется (в силу симметричности распределения относительно M(X) ) равное ему по абсолютной величине отрицательное значение этой величины, причем их вероятности будут одинаковыми.
 Если центральный момент нечетного порядка не равны нулю, то это говорит об асимметричности распределения, причем чем больше момент, тем больше асимметрия. Поэтому в качестве характеристики асимметрии распределения разумнее всего взять какой-нибудь нечетный центральный момент. Так как центральный момент первого порядка всегда равен нулю, то целесообразно для этой цели использовать центральный момент третьего порядка.
Если центральный момент нечетного порядка не равны нулю, то это говорит об асимметричности распределения, причем чем больше момент, тем больше асимметрия. Поэтому в качестве характеристики асимметрии распределения разумнее всего взять какой-нибудь нечетный центральный момент. Так как центральный момент первого порядка всегда равен нулю, то целесообразно для этой цели использовать центральный момент третьего порядка.
Определение 6.12. Коэффициентом асимметрии называется величина:
Если коэффициент асимметрии отрицательный, то это говорит о большом влиянии на величину отрицательных отклонений. В этом случае кривая распределения (рис. 6.1а ) более полога слева от . Если коэффициент положительный, а значит, преобладает влияние положительных отклонений, то кривая распределения более пологая справа.
Как известно, второй центральный момент (дисперсии) служит для характеристики рассеивания значений случайной величины вокруг ее математического ожидания. Если этот момент для некоторой случайной величины достаточно большой, т.е. рассеивание велико, то соответствующая кривая распределения более пологая, чем кривая распределения случайной величины, имеющей меньший момент второго порядка. Однако моментне может служить для этой цели в силу того, что для любого распределения  .
.
В этом случае используется центральный момент четвертого порядка.
Определение 6.13. Эксцессом называется величина:
Для наиболее распространенного в природе нормального закона распределения отношение . Поэтому эксцесс, заданный формулой (6.28) служит для сравнения данного распределения с нормальным (рис. 6.1b ).
Особое значение для характеристики распределения случайной величины имеют числовые характеристики, называемые начальными и центральными моментами.
Начальным моментом k -го порядка α k (Х ) случайной величины Х k -ой степени этой величины, т.е.
α k (Х ) = М (Х k ) (6.8)
Формула (6.8) в силу определения математического ожидания для различных случайных величин имеет свой вид, а именно, для дискретной случайной величины с конечным множеством значений
для непрерывной случайной величины
 , (6.10)
, (6.10)
где f (x ) - плотность распределения случайной величины Х .
Несобственный интеграл в формуле (6.10) превращается в определенный интеграл по конечному промежутку, если значения непрерывной случайной величины имеются только в этом промежутке.
Одна из ранее введенных числовых характеристик – математическое ожидание – является не чем иным, как начальным моментом первого порядка, или, как говорят, первым начальным моментом:
М (Х ) = α 1 (Х ).
В предыдущем пункте было введено понятие центрированной случайной величины Х – М (Х ). Если эту величину рассматривать в качестве основной, то для нее также могут быть найдены начальные моменты. Для самой величины Х эти моменты будут называться центральными.
Центральным моментом k -го порядка μ k (Х ) случайной величины Х называется математическое ожидание k -ой степени центрированной случайной величины, т.е.
μ k (Х ) = М [(Х – М (Х )) k ] (6.11)
Иначе говоря, центральный момент k -го порядка – это математическое ожидание k -ой степени отклонения.
Центральный момент k -го порядка для дискретной случайной величины с конечным множеством значений находится по формуле:
![]() , (6.12)
, (6.12)
для непрерывной случайной величины по формуле:
 (6.13)
(6.13)
В дальнейшем, когда будет понятно о какой случайной величине идет речь, то ее в обозначениях начальных и центральных моментах писать не будем, т.е. вместо α k (Х ) и μ k (Х ) будем писать просто α k и μ k .
Очевидно, что центральный момент первого порядка равен нулю, так как это ни что иное, как математическое ожидание отклонения, которое равно нулю по ранее доказанному, т.е. .
Нетрудно понять, что центральный момент второго порядка случайной величины Х совпадает с дисперсией этой же случайной величины, т.е.
Кроме этого, существуют следующие формулы, связывающие начальные и центральные моменты:

Итак, моменты первого и второго порядков (математическое ожидание и дисперсия) характеризуют самые важные черты распределения: его положение и степень разброса значений. Для более подробного описания распределения служат моменты более высоких порядков. Покажем это.
Предположим, что распределение случайной величины симметрично относительно своего математического ожидания. Тогда все центральные моменты нечетного порядка, если они существуют, равны нулю. Это объясняется тем, что в силу симметричности распределения для каждого положительного значения величины Х − М (Х ) существует равное ему по модулю отрицательное значение, при этом вероятности этих значений равны. Следовательно, сумма в формуле (6.12) состоит из нескольких пар, равных по модулю, но разных по знаку слагаемых, которые при суммировании взаимно уничтожаются. Таким образом, вся сумма, т.е. центральный момент любого нечетного порядка дискретной случайной величины равен нулю. Аналогично, центральный момент любого нечетного порядка непрерывной случайной величины равен нулю, как интеграл в симметричных пределах от нечетной функции.
Естественно предположить, что если центральный момент нечетного порядка отличен от нуля, то и само распределение не будет симметрично относительно своего математического ожидания. При этом, чем больше центральный момент отличается от нуля, тем больше асимметрия в распределении. Возьмем в качестве характеристики асимметрии центральный момент наименьшего нечетного порядка. Так как центральный момент первого порядка равен нулю для случайных величин, имеющих любые распределения, то для этой цели лучше использовать центральный момент третьего порядка. Однако этот момент имеет размерность куба случайной величины. Чтобы избавиться от этого недостатка и перейти к безразмерной случайной величине, делят значение центрального момента на куб среднеквадратического отклонения.
Коэффициентом асимметрии А s или просто асимметрией называется отношение центрального момента третьего порядка к кубу среднеквадратического отклонения, т.е.
Иногда асимметрию называют "скошенностью" и обозначают S k , что происходит от английского слова skew – "косой".
Если коэффициент асимметрии отрицательный, то на его величину достаточно сильно влияние отрицательных слагаемых (отклонений) и распределение будет иметь левую асимметрию , а график (кривая) распределения является более пологим слева от математического ожидания. Если коэффициент положителен, то асимметрия правая , а кривая более полога справа от математического ожидания (рис.6.1).
 |
Как было показано, для характеристики разброса значений случайной величины вокруг своего математического ожидания служит второй центральный момент, т.е. дисперсия. Если этот момент имеет большое числовое значение, то данная случайная величина имеет большой разброс значений и соответствующая кривая распределения имеет более пологий вид, чем кривая, для которой второй центральный момент имеет меньшее значение. Поэтому второй центральный момент характеризует, в какой-то степени, "плосковершинность" или "островершинность" кривой распределения. Однако эта характеристика не очень удобная. Центральный момент второго порядка имеет размерность равную квадрату размерности случайной величины. Если попытаться получить безразмерную величину, поделив значение момента на квадрат среднеквадратического отклонения, то для любой случайной величины получим: ![]() . Таким образом, этот коэффициент не может являться какой-либо характеристикой распределения случайной величины. Он одинаков для всех распределений. В этом случае можно использовать центральный момент четвертого порядка.
. Таким образом, этот коэффициент не может являться какой-либо характеристикой распределения случайной величины. Он одинаков для всех распределений. В этом случае можно использовать центральный момент четвертого порядка.
Эксцессом E k называется величина, определяемая по формуле
![]() (6.15)
(6.15)
Эксцесс, в основном, применяется для непрерывных случайных величин и служит для характеристики, так называемой "крутости" кривой распределения, или иначе, как уже было сказано, для характеристики "плосковершинности" или "островершинности" кривой распределения. В качестве эталонной кривой распределения считается кривая нормального распределения (о нем будет подробно идти речь в следующем главе). Для случайной величины, распределенной по нормальному закону, имеет место равенство . Поэтому эксцесс, заданный формулой (6.15), служит для сравнения данного распределения с нормальным, у которого эксцесс получается равным нулю.
Если для какой-то случайной величины получен положительный эксцесс, то кривая распределения этой величины является более островершинной, чем кривая нормального распределения. Если же эксцесс отрицателен, то кривая является более плосковершинной по сравнению с кривой нормального распределения (рис. 6.2).
 |
Перейдем теперь к конкретным видам законов распределения дискретной и непрерывной случайных величин.
Центральными называются моменты распределения, при вычислении которых за исходную величину принимаются отклонение вариантов от средней арифметической данного ряда.
1. Рассчитаем центральный момент первого порядка по формуле:
2. Рассчитаем центральный момент второго порядка по формуле:

где - значение середины интервалов;
Это среднее взвешенное;
Fi-число значений.
3. Рассчитаем центральный момент третьего порядка по формуле:

где - значение середины интервалов; - это среднее взвешенное; - fi-число значений.
4. Рассчитаем центральный момент четвертого порядка по формуле:

где - значение середины интервалов; - это среднее взвешенное; - fi-число значений.
Расчет для таблицы 3.2
Расчет для таблицы 3.4
1. Рассчитаем центральный момент первого порядка по формуле (7.1):
2. Рассчитаем центральный момент второго порядка по формуле (7.2):
3. Рассчитаем центральный момент третьего порядка по формуле (7.3):
4. Рассчитаем центральный момент четвертого порядка по формуле (7.4):
Расчет для таблицы 3.6
1. Рассчитаем центральный момент первого порядка по формуле (7.1):
2. Рассчитаем центральный момент второго порядка по формуле (7.2):
3. Рассчитаем центральный момент третьего порядка по формуле (7.3):
4. Рассчитаем центральный момент четвертого порядка по формуле (7.4):





Рассчитаны моменты 1,2,3,4 порядков по трем задачам. Где момент третьего порядка понадобиться для расчета асимметрии, а момент четвертого порядка понадобиться для расчета эксцесса.
РАСЧЕТ АСИММЕТРИИ РАСПРЕДЕЛЕНИЯ
В статистической практике встречаются разнообразные распределения. Различают следующие разновидности кривых распределения:
· одновершинные кривые: симметричные, умеренно асимметричные и крайне асимметричные;
· многовершинные кривые.
Для однородных совокупностей, как правило, характерны одновершинные распределения. Многовершинность свидетельствует о неоднородности изучаемой совокупности. Появление двух или более вершин делает необходимой перегруппировку данных с целью выделения более однородных групп.
Выяснение общего характера распределения предполагает оценку его однородности, а также вычисление показателей асимметрии и эксцесса. Для симметричных распределений частоты любых двух вариант, равностоящих в обе стороны от центра распределения, равны между собой. Рассчитанные для таких распределений средняя, мода и медиана также равны.
При сравнительном изучении асимметрии нескольких распределений с разными единицами измерения вычисляется относительный показатель асимметрии ():


где -это среднее взвешенное; Mo-мода; -среднеквадратичная взвешенная дисперсия; Me-медиана.
Его величина может быть положительной и отрицательной. В первом случае речь идет о правосторонней асимметрии, а во втором- о левосторонней.
При правосторонней асимметрии Mo>Me >x. Наиболее широко (как показатель асимметрии) применяется отношение центрального момента третьего порядка к среднему квадратическому отклонению данного ряда в кубе:
где -центральный момент третьего порядка; -среднее квадратическое отклонение в кубе.
Применение данного показателя дает возможность определить не только величину асимметрии, но и проверить ее наличие в генеральной совокупности. Принято считать, что асимметрия выше 0,5 (независимо от знака) считается значительной; если она меньше 0,25, то незначительной.
Оценка существенности производится на основе средней квадратической ошибки, коэффициента асимметрии (), которая зависит от числа наблюдений (n) и рассчитывается по формуле:

где n-число наблюдений.
В случае асимметрия существенна и распределение признака в генеральной совокупности несимметрично. В противном случае асимметрия несущественна и ее наличие может быть вызвано случайными обстоятельствами.
Расчет для таблицы 3.2 Группировка населения по среднемесячной заработной плате, руб.
Левосторонняя, значительная асимметрия.
Расчет для таблицы 3.4 Группировка магазинов по розничному товарообороту, млн. руб.
1. Определим асимметрии по формуле (7.5):
Правосторонняя, значительная асимметрия.
Расчет для таблицы 3.6 Группировка транспортных организаций по грузообороту транспорта общего пользования (млн.т.км)
1. Определим асимметрии по формуле (7.5):
Правосторонняя, незначительная асимметрия.
РАСЧЕТ ЭКСЦЕССА РАСПРЕДЕЛЕНИЯ
Для симметричных распределений может быть рассчитан показатель эксцесса ():

где - центральный момент четвертого порядка; - средне квадратическое отклонение в четвертой степени.
Расчет для таблицы 3.2 Группировка населения по среднемесячной заработной плате, руб.

Расчет для таблицы 3.4 Группировка магазинов по розничному товарообороту, млн. руб.
Рассчитаем показатель эксцесса по формуле (7.7)

Островершинное распределение.
Расчет для таблицы 3.6 Группировка транспортных организаций по грузообороту транспорта общего пользования (млн.т.км)
Рассчитаем показатель эксцесса по формуле (7.7)

Плосковершинное распределение.
ОЦЕНКА ОДНОРОДНОСТИ СОВОКУПНОСТИ
Оценка однородности для таблицы 3.2 Группировка населения по среднемесячной заработной плате, руб.
Необходимо отметить, что хотя показатели асимметрии и эксцесса характеризуют непосредственно лишь форму распределения признака в пределах изучаемой совокупности, однако их определение имеет не только описательное значение. Часто асимметрия и эксцесс дают определенные указания для дальнейшего исследования социально - экономических явлений. Полученный результат свидетельствует о наличии значительной по величине и отрицательной по своему характеру асимметрии, нужно заметить, что асимметрия является левосторонней. Кроме того совокупность имеет плос-ковершинное распределение.
Оценка однородности для таблицы 3.4 Группировка магазинов по розничному товарообороту, млн. руб.
Полученный результат свидетельствует о наличии значительной по величине и положительной по своему характеру асимметрии, нужно заметить что асимметрия является правосторонней. А так же совокупность имеет остро-вершинное распределение.
Оценка однородности для таблицы 3.6 Группировка транспортных организаций по грузообороту транспорта общего пользования (млн.т.км)
Полученный результат свидетельствует о наличии незначительной по величине и положительной по своему характеру асимметрии, нужно заметить что асимметрия является правосторонней. Кроме того совокупность имеет плосковершинное распределение.
Найдем математическое ожидание Х 2 :
М (Х 2) = 1* 0, 6 + 4* 0, 2 + 25* 0, 19+ 10000* 0, 01 = 106, 15.
Видим, что М (X 2) значительно больше М (X ). Это объясняется тем, что после возведения в квадрат возможное значение величины X 2 , соответствующее значению x =100 величины X, стало равным 10 000, т. е. значительно увеличилось; вероятность же этого значения мала (0,01).
Таким образом, переход от М (X )к М (X 2)позволил лучше учесть влияние на математическое ожидание того возможного значения, которое велико и имеет малую вероятность. Разумеется, если бы величина X имела несколько больших и маловероятных значений, то переход к величине X 2 , а тем более к величинам X 3 , X 4 и т. д., позволил бы еще больше «усилить роль» этих больших, но маловероятных возможных значений. Вот почему оказывается целесообразным рассматривать математическое ожидание целой положительной степени случайной величины (не только дискретной, но и непрерывной).
Начальным моментом порядка k случайной величины X называют математическое ожидание величины X k:
v k = M (X ).
В частности,
v 1 = M (X ), v 2 = M (X 2).
Пользуясь этими моментами, формулу для вычисления дисперсии D (X ) = M (X 2)- [М (X )] 2 можно записать так:
D (X )= v 2 – . (*)
Кроме моментов случайной величины X целесообразно рассматривать моменты отклонения X-М (X ).
Центральным моментом порядка k случайной величины X называют математическое ожидание величины (Х-М (Х )) k:
В частности,
Легко выводятся соотношения, связывающие начальные и центральные моменты. Например, сравнивая (*) и (***), получим
m 2= v 2 – .
Нетрудно, исходя из определения центрального момента и пользуясь свойствами математического ожидания, получить формулы:
m 3= v 3 – 3 v 2 v 1 + 2 ,
m 4= v 4 – 4 v 3 v 1 + 6 v 2 + 3 .
Моменты более высоких порядков применяются редко.
Замечание. Моменты, рассмотренные здесь, называют теоретическими. В отличие от теоретических моментов, моменты, которые вычисляются по данным наблюдений, называют эмпирическими. Определения эмпирических моментов даны далее (см. гл. XVII, § 2).
Задачи
1. Известны дисперсии двух независимых случайных величин: D (X ) = 4, D (Y )=3. Найти дисперсию суммы этих величин.
Отв. 7.
2. Дисперсия случайной величины X равна 5. Найти дисперсию следующих величин: а) X -1; б) -2Х; в) ЗХ + 6.
Отв. а) 5; б) 20; в) 45.
3. Случайная величина X принимает только два значения: +С и -С, каждое с вероятностью 0,5. Найти дисперсию этой величины.
Отв. С 2 .
4. , зная закон ее распределения
| X | 0, 1 | |||
| P | 0, 4 | 0, 2 | 0, 15 | 0, 25 |
Отв. 67,6404.
5. Случайная величина X может принимать два возможных значения: х 1 с вероятностью 0,3 и x 2 с вероятностью 0,7, причем х 2 > х 1 . Найти x 1 и x 2 , зная, что М (Х ) = 2, 7и D (X ) =0,21.
Отв. x 1 = 2, x 2 = 3.
6. Найти дисперсию случайной величины X -числа появлений событий А в двух независимых испытаниях, если М (Х ) = 0, 8.
Указание. Написать биномиальный закон распределения вероятностей числа появлений события А в двух независимых испытаниях.
Отв. 0, 48.
7. Испытывается устройство, состоящее из четырех независимо работающих приборов. Вероятности отказа приборов таковы: р 1 = 0,3; р 2 = 0,4; p 3 = 0,5; р 4 = 0,6. Найти математическое ожидание и дисперсию числа отказавших приборов.
Отв. 1,8; 0,94.
8. Найти дисперсию случайной величины X - числа появлений события в 100 независимых испытаниях, в каждом из которых вероятность наступления события равна 0,7.
Отв. 21.
9. Дисперсия случайной величины D (Х ) = 6,25. Найти среднее квадратическое отклонение s(X ).
Отв. 2, 5.
10. Случайная величина задана законом распределения
| X | |||
| P | 0, 1 | 0, 5 | 0, 4 |
Найти среднее квадратическое отклонение этой величины.
Отв. 2, 2.
11. Дсперсия каждой из 9 одинаково распределенных взаимно независимых случайных величин равна 36. Найти дисперсию среднего арифметического этих величин.
Отв. 4.
12. Среднее квадратическое отклонение каждой из 16 одинаково распределенных взаимно независимых случайных величин равно 10. Найти среднее квадратическое отклонение среднего арифметического этих величин.
Отв. 2,5.
Глава девятая
ЗАКОН БОЛЬШИХ ЧИСЕЛ
Предварительные замечания
Как уже известно, нельзя заранее уверенно предвидеть, какое из возможных значений примет случайная величина в итоге испытания; это зависит от многих случайных причин, учесть которые невозможно. Казалось бы, поскольку о каждой случайной величине мы располагаем в этом смысле весьма скромными сведениями, то вряд ли можно установить закономерности поведения и суммы достаточно большого числа случайных величин. На самом деле это не так. Оказывается, что при некоторых сравнительно широких условиях суммарное поведение достаточно большого числа случайных величин почти утрачивает случайный характер и становится закономерным.
Для практики очень важно знание условий, при выполнении которых совокупное действие очень многих случайных причин приводит к результату, почти не зависящему от случая, так как позволяет предвидеть ход явлений. Эти условия и указываются в теоремах, носящих общее название закона больших чисел. К ним относятся теоремы Чебышева и Бернулли (имеются и другие теоремы, которые здесь не рассматриваются). Теорема Чебышева является наиболее общим законом больших чисел, теорема Бернулли-простейшим. Для доказательства этих теорем мы воспользуемся неравенством Чебышева.
Неравенство Чебышева
Неравенство Чебышева справедливо для дискретных и непрерывных случайных величин. Для простоты ограничимся доказательством этого неравенства для дискретных величин.
Рассмотрим дискретную случайную величину X, заданную таблицей распределения:
| X | x 1 | X 2 | … | x n |
| p | p 1 | P 2 | … | p n |
Поставим перед собой задачу оценить вероятность того, что отклонение случайной величины от ее математического ожидания не превышает по абсолютной величине положительного числа e. Если e достаточно мало, то мы оценим, таким образом, вероятность того, что X примет значения, достаточно близкие к своему математическому ожиданию. П. Л. Чебышев доказал неравенство, позволяющее дать интересующую нас оценку.
Неравенство Чебышева. Вероятность того, что отклонение случайной величины X от ее математического ожидания по абсолютной величине меньше положительного числа e, не меньше, чем 1-D (Х )/ e 2 :
Р (|Х -М (Х )|< e ) 1-D (X )/ e 2 .
Доказательство. Так как события, состоящие в осуществлении неравенств |Х-М
(Х
)|
Р (|Х -М (Х )|< e )+ Р (|Х -М (Х )| e )= 1.
Отсюда интересующая нас вероятность
Р (|Х -М (Х )|< e )= 1- Р (|Х -М (Х )| e ). (*)
Таким образом, задача сводится к вычислению вероятности Р (| Х-М (Х ) | e ).
Напишем выражение дисперсии случайной величины X :
D (X )= [x 1 -M (X )] 2 p 1 + [x 2 -M (X )] 2 p 2 +…+ [x n -M (X )]2p n .
Очевидно, все слагаемые этой суммы неотрицательны.
Отбросим те слагаемые, у которых |x i -M (Х )|< e (для оставшихся слагаемых |x j -M (Х )| e ), вследствие чего сумма может только уменьшиться. Условимся считать для определенности, что отброшено k первых слагаемых (не нарушая общности, можно считать, что в таблице распределения возможные значения занумерованы именно в таком порядке). Таким образом,
D (X ) [x k + 1 -M (Х )] 2 p k + 1 + [x k + 2 -M (X )] 2 p k + z + . .. +[x n -M (X )] 2 p n .
Заметим, что обе части неравенства |x j - М (Х )| e (j = k +1, k + 2, ..., п )положительны, поэтому, возведя их в квадрат, получим равносильное неравенство |x j - М (Х )| 2 e 2 Воспользуемся этим замечанием и, заменяя в оставшейся сумме каждый из множителей |x j - М (Х )| 2 числом e 2 (при этом неравенство может лишь усилиться), получим
D (X ) e 2 (р к+ 1 + p k + 2 + … + р n ). (**)
По теореме сложения, сумма вероятностей р к+ 1 + p k + 2 + … + р n есть вероятность того, что X примет одно, безразлично какое, из значений x k + 1 , х к+ 2 ,....х п, а при любом из них отклонение удовлетворяет неравенству |x j - М (Х )| e Отсюда следует, что сумма р к+ 1 + p k + 2 + … + р n выражает вероятность
P (|X - М (Х )| e).
Это соображение позволяет переписать неравенство (**) так:
D (X ) e 2 P (|X - М (Х )| e) ,
P (|X - М (Х )| e) D (X ) / e 2 (***)
Подставляя (***) в (*), окончательно получим
P (|X - М (Х )| <e) 1- D (X ) / e 2 ,
что и требовалось доказать.
Замечание. Неравенство Чебышева имеет для практики ограниченное значение поскольку часто дает грубую, а иногда и тривиальную (не представляющую интереса) оценку. Например, если D (X )> e 2 и, следовательно, D (X )/ e 2 > 1, то 1- D (Х )/ e 2 < 0; таким образом, в этом случае неравенство Чебышева указывает лишь на то, что вероятность отклонения неотрицательна, а это и без того очевидно, так как любая вероятность выражается неотрицательным числом.
Теоретическое же значение неравенства Чебышева весьма велико. Ниже мы воспользуемся этим неравенством для вывода теоремы Чебышева.
Теорема Чебышева
Теорема Чебышева. Если Х 1 , Х 2 ,…, Х n , ... -попарно независимые случайные величины, причем дисперсии их равномерно ограничены (не превышают постоянного числа С ), то, как бы мало ни было положительное число е, вероятность неравенства
Другими словами, в условиях теоремы
Таким образом, теорема Чебышева утверждает, что если рассматривается достаточно большое число независимых случайных величин, имеющих ограниченные дисперсии, то почти достоверным можно считать событие, состоящее в том, что отклонение среднего арифметического случайных величин от среднего арифметического их математических ожиданий будет по абсолютной величине сколь угодно малым.
Доказательство. Введем в рассмотрение новую случайную величину - среднее арифметическое случайных величин
=(X 1 +X 2 +…+X n )/n.
Найдем математическое ожидание . Пользуясь свойствами математического ожидания (постоянный множитель можно вынести за знак математического ожидания, математическое ожидание суммы равно сумме математических ожиданий слагаемых), получим
M ![]() =
=
![]() . (*)
. (*)
Применяя к величине неравенство Чебышева, имеем
Подставляя правую часть (***) в неравенство (**) (отчего последнее может быть лишь усилено), имеем
Отсюда, переходя к пределу при , получим
Наконец, учитывая, что вероятность не может превышать единицу, окончательно можем написать
Теорема доказана.
Выше, формулируя теорему Чебышева, мы предполагали, что случайные величины имеют различные математические ожидания. На практике часто бывает, что случайные величины имеют одно и то же математическое ожидание. Очевидно, что если вновь допустить, что дисперсии этих величин ограничены, то к ним будет применима теорема Чебышева.
Обозначим математическое ожидание каждой из случайных величин через а; в рассматриваемом случае среднее арифметическое математических ожиданий, как легко видеть, также равно а. Мы можем сформулировать теорему Чебышева для рассматриваемого частного случая.
Если Х 1 , Х 2 , ..., Х п,... -попарно независимые случайные величины, имеющие одно и то же математическое ожидание а, и если дисперсии этих величин равномерно ограничены, то, как бы мало ни было число e > О, вероятность неравенства
![]()
будет как угодно близка к единице, если число случайных величин достаточно велико.
Другими словами, в условиях теоремы будет иметь место равенство

Сущность теоремы Чебышева
Сущность доказанной теоремы такова: хотя отдельные независимые случайные величины могут принимать значения, далекие от своих математических ожиданий, среднее арифметическое достаточно большого числа случайных величин с большой вероятностью принимает значения, близкие к определенному постоянному числу, а именно к числу (М (X 1)+ М (Х 2) +...+М (Х п ))/п (или к числу а в частном случае). Иными словами, отдельные случайные величины могут иметь значительный разброс, а их среднее арифметическое рассеянно мало.
Таким образом, нельзя уверенно предсказать, какое возможное значение примет каждая из случайных величин, но можно предвидеть, какое значение примет их среднее арифметическое.
Итак, среднее арифметическое достаточно большого числа независимых случайных величин (дисперсии которых равномерно ограничены) утрачивает характер случайной величины. Объясняется это тем, что отклонения каждой из величин от своих математических ожиданий могут быть как положительными, так и отрицательными, а в среднем арифметическом они взаимно погашаются.
Теорема Чебышева справедлива не только для дискретных, но и для непрерывных случайных величин; она является ярким примером, подтверждающим справедливость учения диалектического материализма о связи между случайностью и необходимостью.